Drop rates: Difference between revisions
No edit summary |
|||
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
=== What is the chance of dropping a reward? === | === What is the chance of dropping a reward? === | ||
On many of the [[guides]] you will see the drop-rate for a particular reward given. This will typically be expressed as a fraction | On many of the [[guides]] you will see the drop-rate for a particular reward given. This will typically be expressed as a fraction or a percentage. For example, the rate of drop-rate for the {{ItemIcon|Chapeau Noir}} in {{Skill|Thieving}} is 1/20,000 (0.005%). | ||
The drop-rate of the reward shows you probability of the item dropping, but it is not the same as the chance of the reward being given. For example, if you were to perform this action 20,000 times you might reasonably expect to get this item, however, there is only a 63% chance of this happening. | The drop-rate of the reward shows you probability of the item dropping, but it is not the same as the chance of the reward being given. For example, if you were to perform this action 20,000 times you might reasonably expect to get this item, however, there is only a 63% chance of this happening. | ||
| Line 20: | Line 20: | ||
It might be surprising to learn that farming for rare items is often going to take considerably longer than you may have initially thought based on the drop-rate. Of course, you might get lucky and drop this reward on your first attempt! | It might be surprising to learn that farming for rare items is often going to take considerably longer than you may have initially thought based on the drop-rate. Of course, you might get lucky and drop this reward on your first attempt! | ||
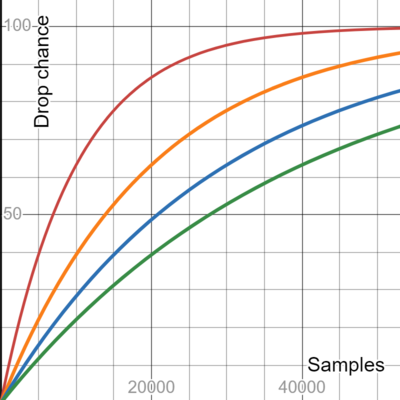
== Visual representation of drop rates == | |||
To visualize what this means, here is a graph showing four different drop rates: | |||
[[File:Visualized_binomial_drop_rates.png|400px]] | |||
{| class="wikitable" | |||
|- | |||
! Drop rate !! Color !! #Attempts for 80% Chance | |||
|- | |||
| 1/10,000 || Red || 16,000 | |||
|- | |||
| 1/20,000 || Orange || 32,000 | |||
|- | |||
| 1/30,000 || Blue || 48,000 | |||
|- | |||
| 1/40,000 || Green || 64,500 | |||
|} | |||
So keep grinding, and see the next section for some of the math behind the probabilities of drops. | So keep grinding, and see the next section for some of the math behind the probabilities of drops. | ||
| Line 29: | Line 48: | ||
<math>P = 1 - \left ( 1 - \dfrac{1}{k} \right ) ^ {n} </math> | <math>P = 1 - \left ( 1 - \dfrac{1}{k} \right ) ^ {n} </math> | ||
If the drop-rate is low | If the drop-rate is low (which ''is'' typical for rare drops) then you can approximate this as: | ||
<math>P \approx 1 - \left ( \dfrac{1}{2.718} \right ) ^ {\left ( \dfrac{n}{k} \right )}</math> | <math>P \approx 1 - \left ( \dfrac{1}{2.718} \right ) ^ {\left ( \dfrac{n}{k} \right )}</math> | ||
| Line 39: | Line 58: | ||
This means that you have a 0.5% chance of discovering at least one of these after 100 attempts. | This means that you have a 0.5% chance of discovering at least one of these after 100 attempts. | ||
== Calculating the number of attempts == | |||
The number of attempts (n) for a given drop-rate (k) with a certain probability (P) is given by: | |||
<math>n = \left \lceil \dfrac {ln(1 - P)} {\ln \left (\dfrac{(k - 1)}{k} \right )} \right \rceil</math> | |||
For those unfamiliar with math notation, the outer brackets just mean take the largest whole number. | |||
If the drop-rate is low which ''is'' typical for rare drops then you can approximate this as: | |||
<math>n \approx \left \lceil -k \cdot \ln(1 - P) \right \rceil</math> | |||
For example, for the {{ItemIcon|Chapeau Noir}} there is a 1 in 20,000 (k) chance of this item dropping, and we want a 75% chance of getting at least one, then we would need: | |||
<math>n \approx \left \lceil -20,000 \cdot \ln(1 - 0.75) \right \rceil = 27,726</math> | |||
This means that you would need 27,726 attempts to give you a 75% chance of discovering that item. | |||
== Further reading == | |||
Further information can be found: | |||
* Online [https://dropchance.app calculators] that you can use to calculate drop-rates. | |||
* Information on the [https://en.wikipedia.org/wiki/Binomial_distribution Binomial Distribution]. | |||
Latest revision as of 19:55, 31 March 2024
What is the chance of dropping a reward?
On many of the guides you will see the drop-rate for a particular reward given. This will typically be expressed as a fraction or a percentage. For example, the rate of drop-rate for the ![]() Chapeau Noir in
Chapeau Noir in
is 1/20,000 (0.005%).
The drop-rate of the reward shows you probability of the item dropping, but it is not the same as the chance of the reward being given. For example, if you were to perform this action 20,000 times you might reasonably expect to get this item, however, there is only a 63% chance of this happening.
For example, the chances for the ![]() Chapeau Noir to drop at least once for a given number of attempts can be seen on this table.
Chapeau Noir to drop at least once for a given number of attempts can be seen on this table.
| Chance of success | Number of attempts |
|---|---|
| 50% | 13,863 |
| 90% | 46,051 |
| 99% | 92,102 |
It might be surprising to learn that farming for rare items is often going to take considerably longer than you may have initially thought based on the drop-rate. Of course, you might get lucky and drop this reward on your first attempt!
Visual representation of drop rates
To visualize what this means, here is a graph showing four different drop rates:
| Drop rate | Color | #Attempts for 80% Chance |
|---|---|---|
| 1/10,000 | Red | 16,000 |
| 1/20,000 | Orange | 32,000 |
| 1/30,000 | Blue | 48,000 |
| 1/40,000 | Green | 64,500 |
So keep grinding, and see the next section for some of the math behind the probabilities of drops.
Calculating the chance of drops
The probability (P) for a given drop-rate (k) over a fixed number of attempts (n) is given by:
[math]\displaystyle{ P = 1 - \left ( 1 - \dfrac{1}{k} \right ) ^ {n} }[/math]
If the drop-rate is low (which is typical for rare drops) then you can approximate this as:
[math]\displaystyle{ P \approx 1 - \left ( \dfrac{1}{2.718} \right ) ^ {\left ( \dfrac{n}{k} \right )} }[/math]
For example, for the ![]() Chapeau Noir there is a 1 in 20,000 (k) chance of this item dropping, and 100 attempts gives a probability of:
Chapeau Noir there is a 1 in 20,000 (k) chance of this item dropping, and 100 attempts gives a probability of:
[math]\displaystyle{ P = 1 - \left ( 1 - \dfrac{1}{20,000} \right ) ^ {100} = 0.005 = 0.5 \% }[/math]
This means that you have a 0.5% chance of discovering at least one of these after 100 attempts.
Calculating the number of attempts
The number of attempts (n) for a given drop-rate (k) with a certain probability (P) is given by:
[math]\displaystyle{ n = \left \lceil \dfrac {ln(1 - P)} {\ln \left (\dfrac{(k - 1)}{k} \right )} \right \rceil }[/math]
For those unfamiliar with math notation, the outer brackets just mean take the largest whole number.
If the drop-rate is low which is typical for rare drops then you can approximate this as:
[math]\displaystyle{ n \approx \left \lceil -k \cdot \ln(1 - P) \right \rceil }[/math]
For example, for the ![]() Chapeau Noir there is a 1 in 20,000 (k) chance of this item dropping, and we want a 75% chance of getting at least one, then we would need:
Chapeau Noir there is a 1 in 20,000 (k) chance of this item dropping, and we want a 75% chance of getting at least one, then we would need:
[math]\displaystyle{ n \approx \left \lceil -20,000 \cdot \ln(1 - 0.75) \right \rceil = 27,726 }[/math]
This means that you would need 27,726 attempts to give you a 75% chance of discovering that item.
Further reading
Further information can be found:
- Online calculators that you can use to calculate drop-rates.
- Information on the Binomial Distribution.